TypeScriptを活用してグラフ理論を学ぶことは、理論の理解を深めるだけでなく、プログラミングスキルの向上にもつながります。本記事では、TypeScriptを使用したグラフの基本的な実装からアルゴリズムの適用例までを解説します。
グラフ理論ってなに?というところからおさらいしたい方は以下の記事を参照してください。
[目次を開く]
1. TypeScriptでグラフを実装する
隣接リストの実装
隣接リストは、メモリ効率が高く、スパースグラフに適しています。TypeScriptで隣接リストを実装する方法を以下に示します。
class Graph {
private adjacencyList: Map<string, string[]>;
constructor() {
this.adjacencyList = new Map();
}
addVertex(vertex: string): void {
if (!this.adjacencyList.has(vertex)) {
this.adjacencyList.set(vertex, []);
}
}
addEdge(vertex1: string, vertex2: string): void {
this.adjacencyList.get(vertex1)?.push(vertex2);
this.adjacencyList.get(vertex2)?.push(vertex1); // 無向グラフの場合
}
displayGraph(): void {
for (const [vertex, edges] of this.adjacencyList) {
console.log(`${vertex} -> ${edges.join(", ")}`);
}
}
}
// 使用例
const graph = new Graph();
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.displayGraph();
上記のコードでは、頂点を追加し、それらを結ぶ辺を作成しています。グラフ全体を隣接リストの形式で出力可能です。
上記のコードのイメージ
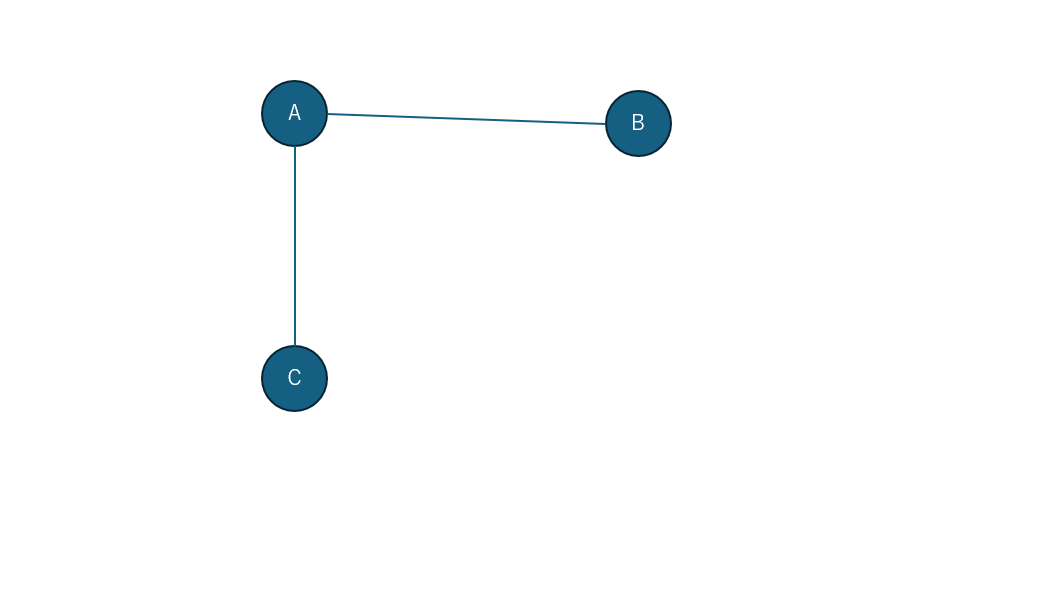
グラフ理論におけるノードは、ドットや丸で表します。ノード間の接続はエッジと呼ばれる線で表現されます。
2. 基本アルゴリズムの実装
深さ優先探索(DFS)
深さ優先探索は、再帰を用いることで簡潔に実装できます。
class DFSGraph extends Graph {
dfs(start: string): void {
const visited = new Set<string>();
const dfsHelper = (vertex: string) => {
if (!vertex || visited.has(vertex)) return;
visited.add(vertex);
console.log(vertex);
for (const neighbor of this.adjacencyList.get(vertex) || []) {
dfsHelper(neighbor);
}
};
dfsHelper(start);
}
}
// 使用例
const dfsGraph = new DFSGraph();
dfsGraph.addVertex("A");
dfsGraph.addVertex("B");
dfsGraph.addVertex("C");
dfsGraph.addEdge("A", "B");
dfsGraph.addEdge("A", "C");
dfsGraph.dfs("A");
幅優先探索(BFS)
BFSはキューを使用して、各層ごとに探索を進めます。
class BFSGraph extends Graph {
bfs(start: string): void {
const visited = new Set<string>();
const queue: string[] = [start];
while (queue.length > 0) {
const vertex = queue.shift()!;
if (!visited.has(vertex)) {
visited.add(vertex);
console.log(vertex);
for (const neighbor of this.adjacencyList.get(vertex) || []) {
if (!visited.has(neighbor)) {
queue.push(neighbor);
}
}
}
}
}
}
// 使用例
const bfsGraph = new BFSGraph();
bfsGraph.addVertex("A");
bfsGraph.addVertex("B");
bfsGraph.addVertex("C");
bfsGraph.addEdge("A", "B");
bfsGraph.addEdge("A", "C");
bfsGraph.bfs("A");
3. 応用アルゴリズムの実装
ダイクストラ法(最短経路探索)
重み付きグラフを用いた最短経路アルゴリズムです。
class WeightedGraph {
private adjacencyList: Map<string, [string, number][]>;
constructor() {
this.adjacencyList = new Map();
}
addVertex(vertex: string): void {
if (!this.adjacencyList.has(vertex)) {
this.adjacencyList.set(vertex, []);
}
}
addEdge(vertex1: string, vertex2: string, weight: number): void {
this.adjacencyList.get(vertex1)?.push([vertex2, weight]);
this.adjacencyList.get(vertex2)?.push([vertex1, weight]);
}
dijkstra(start: string, finish: string): void {
const distances: { [key: string]: number } = {};
const previous: { [key: string]: string | null } = {};
const queue: [string, number][] = [];
for (const vertex of this.adjacencyList.keys()) {
if (vertex === start) {
distances[vertex] = 0;
queue.push([vertex, 0]);
} else {
distances[vertex] = Infinity;
}
previous[vertex] = null;
}
while (queue.length) {
const [currentVertex] = queue.shift()!;
if (currentVertex === finish) break;
for (const [neighbor, weight] of this.adjacencyList.get(currentVertex) || []) {
const distance = distances[currentVertex] + weight;
if (distance < distances[neighbor]) {
distances[neighbor] = distance;
previous[neighbor] = currentVertex;
queue.push([neighbor, distance]);
}
}
}
console.log("最短経路の距離:", distances[finish]);
}
}
// 使用例
const weightedGraph = new WeightedGraph();
weightedGraph.addVertex("A");
weightedGraph.addVertex("B");
weightedGraph.addVertex("C");
weightedGraph.addVertex("D");
weightedGraph.addVertex("E");
weightedGraph.addVertex("F");
weightedGraph.addEdge("A", "B", 4);
weightedGraph.addEdge("A", "C", 2);
weightedGraph.addEdge("C", "D", 3);
weightedGraph.addEdge("C", "D", 3);
weightedGraph.addEdge("D", "E", 1);
weightedGraph.addEdge("B", "F", 2);
weightedGraph.addEdge("E", "F", 3);
weightedGraph.dijkstra("A", "F");
上記のコードのイメージ
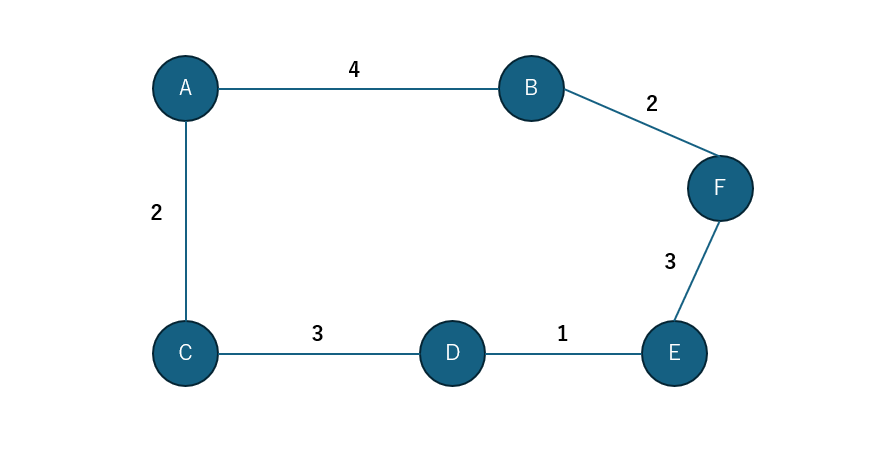
weightedGraph.dijkstra("A", "F"); で頂点Aから頂点Fまでの最短経路を出力します。
4. 学習の次のステップ
TypeScriptを使用してグラフ理論を学ぶ際は、以下の点にも取り組むと良いでしょう:
- 実践課題
- 実際の交通ネットワークやソーシャルグラフをモデリングして、アルゴリズムを試します。
- ライブラリを活用
- D3.jsやGraphlibなどのグラフライブラリを組み合わせて視覚化に挑戦します。
- 応用アルゴリズム
- クラスカル法やフロイド・ワーシャル法など、高度なアルゴリズムを実装します。
まとめ
TypeScriptを使用したグラフ理論の学習は、実際にコードを書きながら理論を深く理解できるため、非常に効果的です。データ構造とアルゴリズムの知識を実践に活用し、問題解決能力を向上させましょう。




